1. 시계열분석 간단정리
정상 시계열의 조건
- 일정한 평균
- 일정한 분산
- 공분산은 t가 아닌 s에 의존
일변량 시계열분석
- 자기회귀모형(AR), 이동평균(MA), Box-Jenkins(ARMA), 지수 평활법, 시계열 분해법 등
2. 예제: 영국 왕들의 사망시 나이 데이터 예측
https://rpubs.com/ryankelly/ts6
RPubs - TimeSeriesAnalysisExamples
rpubs.com
kings<-scan('http://robjhyndman.com/tsdldata/misc/kings.dat', skip=3)
kings<-ts(kings)
plot.ts(kings)
단순이동평균
시계열 데이터를 3년마다 평균을 내어 표현한다.
kingsSMA3<-SMA(kings, n=3)
plot.ts(kingsSMA3)
ARIMA 모델 구축 전 차분 진행
ARIMA는 정상시계열에 한해 사용할 수 있다. 위처럼 평균과 분산이 일정하지 않은 비정상시계열은 차분을 통해 정상시계열의 조건을 만족시켜준다.
king.ff1<-diff(kings, differences=1)
plot.ts(king.ff1)
자기상관함수(ACF)와 편자기상관함수(PACF)를 통한 ARIMA 모델 결정
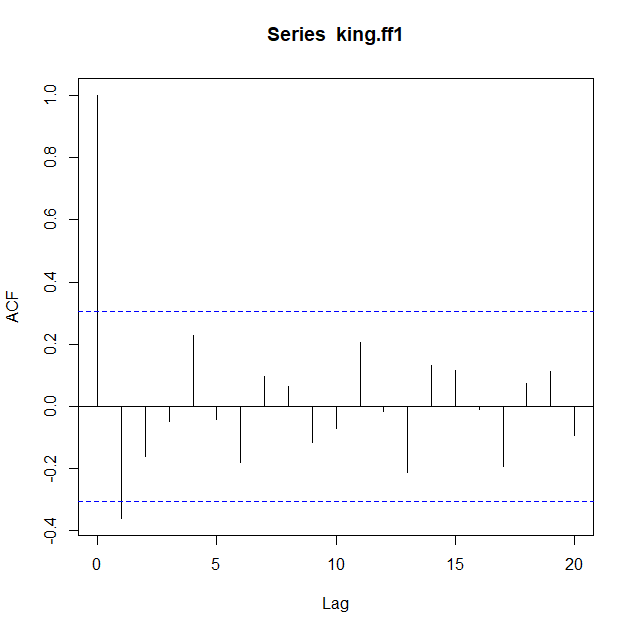
ACF값을 살펴본 결과, lag1인 지점을 제외하고 모두 점선 구간 안에 위치해있다.
acf(king.ff1, lag.max=20)
acf(king.ff1, lag.max=20, plot=FALSE)
##Autocorrelations of series ‘king.ff1’, by lag
##
## 0 1 2 3 4 5 6 7 8 9 10
## 1.000 -0.360 -0.162 -0.050 0.227 -0.042 -0.181 0.095 0.064 -0.116 -0.071
## 11 12 13 14 15 16 17 18 19 20
## 0.206 -0.017 -0.212 0.130 0.114 -0.009 -0.192 0.072 0.113 -0.093
PACF값을 살펴보면, lag3까지 점선 구간을 초과하여 절단점은 lag4이다.
pacf(king.ff1, lag.max=20)
pacf(king.ff1, lag.max=20, plot=FALSE)
##Partial autocorrelations of series ‘king.ff1’, by lag
##
## 1 2 3 4 5 6 7 8 9 10 11
##-0.360 -0.335 -0.321 0.005 0.025 -0.144 -0.022 -0.007 -0.143 -0.167 0.065
## 12 13 14 15 16 17 18 19 20
## 0.034 -0.161 0.036 0.066 0.081 -0.005 -0.027 -0.006 -0.037
위 결과를 통해 ARMA의 후보들을 생각해보면, ARMA(3, 0), ARMA(0, 1)를 들 수 있다.
auto.arima()를 통한 적절한 ARIMA모형 찾기
영국 왕의 사망 나이 데이터의 적절한 모형은 ARIMA(0, 1, 1)
auto.arima(kings)
##Series: kings
##ARIMA(0,1,1)
##
##Coefficients:
## ma1
## -0.7218
##s.e. 0.1208
##
##sigma^2 estimated as 236.2: log likelihood=-170.06
##AIC=344.13 AICc=344.44 BIC=347.56예측
43~47번째 왕의 나이를 예측한 결과 67.75살로 추정된다.
king.arima<-arima(kings, order=c(0, 1, 1))
king.forecasts<-forecast(king.arima, h=5)
king.forecasts
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
##43 67.75063 48.29647 87.20479 37.99806 97.50319
##44 67.75063 47.55748 87.94377 36.86788 98.63338
##45 67.75063 46.84460 88.65665 35.77762 99.72363
##46 67.75063 46.15524 89.34601 34.72333 100.77792
##47 67.75063 45.48722 90.01404 33.70168 101.79958
3. 예제: Air Passenger numbers 예측
Kaggle의 Air Passenger에 대한 1949년부터 1961까지의 데이터를 이용했다. 계절성이 있고, 분산이 점점 커지는 것을 확인할 수 있다.
air<-read.csv('AirPassengers.csv')
air.ts<-ts(air[,2], frequency=12)
plot(air.ts, main='Air Passenger numbers from 1949 to 1961')
시계열분해(Time Series Decomposition)
decompose함수를 통해 시계열 자료를 trend, seasonal, random components로 분해할 수 있다. 분해를 진행한 자료에 $random을 붙이면 random components만 따로 뽑아낼 수 있다.
decomposeAP<-decompose(air.ts, 'multiplicative')
autoplot(decomposeAP)
시계열의 정상성 검정
시계열의 정상성을 검정하기 위해서는 ADF test를 이용하는 방법, 영국왕 사망나이 예측에서 처럼 자기상관성(Autocorrelation)을 통해 검정하는 방법이 있다.
adf.test(air.ts)
## Augmented Dickey-Fuller Test
##
##data: air.ts
##Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01
##alternative hypothesis: stationary먼저 ADF test를 시행해본 결과, p-value가 0.01로 시계열 데이터가 비정상성이라는 귀무가설을 기각하게 된다. 하지만 ADF test만으로는 계절성을 파악할 수 없으므로 adf와 pacf를 추가로 살펴본다.
ggtsdisplay(air.ts)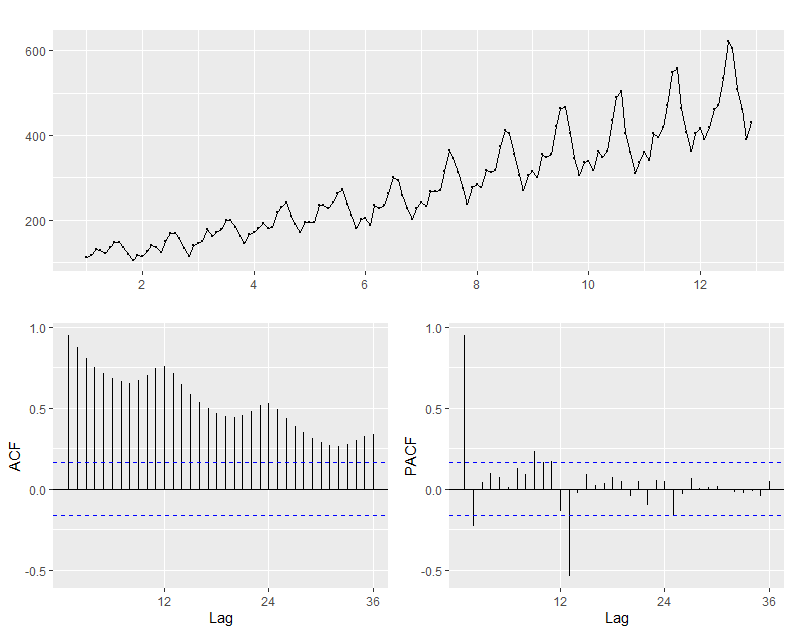
auto.arima를 통한 ARIMA 모형 구축
auto.arima(air.ts)
##Series: air.ts
##ARIMA(2,1,1)(0,1,0)[12]
##
##Coefficients:
## ar1 ar2 ma1
## 0.5960 0.2143 -0.9819
##s.e. 0.0888 0.0880 0.0292
##
##sigma^2 estimated as 132.3: log likelihood=-504.92
##AIC=1017.85 AICc=1018.17 BIC=1029.3512주기의 계절성과 1차 차분이 포함된 arima모델이 구축되었다.
forecastAP<-forecast(auto.arima(air.ts), level=c(95), h=36)
autoplot(forecastAP)
모델 평가
checkresiduals함수를 통해 시계열 모형의 잔차로 모델 평가를 할 수 있다. 시계열 모형의 경우 Ljung-Box 검정 결과를 볼 수 있는데, acf 그림에서는 약간 튀는 값들이 보이지만 p-value가 0.01인 것으로 보아 크게 문제가 되는 수준은 아닌 것으로 보인다
checkresiduals(auto.arima(air.ts))
## Ljung-Box test
##
##data: Residuals from ARIMA(2,1,1)(0,1,0)[12]
##Q* = 37.784, df = 21, p-value = 0.01366
##
##Model df: 3. Total lags used: 24.
'2. 데이터 분석 > ADP' 카테고리의 다른 글
| [R] Catboost 이론 (0) | 2021.09.04 |
|---|