앞서 살펴본 릿지회귀, 라쏘회귀, 주성분회귀 등은 선형모델의 복잡도를 줄여 추정치들의 분산을 줄인다. 하지만 여전히 선형모델이 사용되므로 개선은 한정적이다.
해석력은 여전히 높게 유지하면서 선형성에 대한 가정은 완화하고자 이를 위해 다음과 같은 선형 모델과 기법들을 살펴본다.
- 다항식회귀: 원래의 설명변수 각각을 거듭제곱하여 얻은 추가적인 설명변수들을 포함하여 선형모델을 확장한다. 예를 들어, 삼차회귀는 세 개의 변수 X, X^2, X^3을 설명변수로서 사용한다. 이 기법은 데이터에 대한 비선형적합을 제공하는 방법이다.
- 계단함수: 변수의 범위를 K개 영역으로 구분하여 질적 변수를 생성한다. 이것은 조각별 상수함수를 적합하는 효과를 가진다.
- 회귀 스플라인: 다항식 함수와 계단함수보다 더 유연하며 사실상 이 두 함수의 확장이다.
- 평활 스플라인: 회귀 스플라인과 유사하지만 평활 스플라인은 평활도 페널티 조건하에서 잔차제곱합 기준을 최소로 한 결과이다.
- 국소회귀: 스플라인과 유사하지만 영역들이 겹쳐질 수 있다.
- 일반화가법모델: 다중 설명변수들을 다룰 수 있도록 위에서 설명한 방법들을 확장할 수 있다.
R Code
다항식회귀와 계단함수
library(ISLR)
attach(Wage)
fit=lm(wage~poly(age, 4), data=Wage)
coef(summary(fit))
## Estimate Std. Error t value Pr(>|t|)
##(Intercept) 111.70361 0.7287409 153.283015 0.000000e+00
##poly(age, 4)1 447.06785 39.9147851 11.200558 1.484604e-28
##poly(age, 4)2 -478.31581 39.9147851 -11.983424 2.355831e-32
##poly(age, 4)3 125.52169 39.9147851 3.144742 1.678622e-03
##poly(age, 4)4 -77.91118 39.9147851 -1.951938 5.103865e-02
fit=lm(wage~poly(age, 4, raw=T), data=Wage)
coef(summary(fit))
## Estimate Std. Error t value Pr(>|t|)
##(Intercept) -1.841542e+02 6.004038e+01 -3.067172 0.0021802539
##poly(age, 4, raw = T)1 2.124552e+01 5.886748e+00 3.609042 0.0003123618
##poly(age, 4, raw = T)2 -5.638593e-01 2.061083e-01 -2.735743 0.0062606446
##poly(age, 4, raw = T)3 6.810688e-03 3.065931e-03 2.221409 0.0263977518
##poly(age, 4, raw = T)4 -3.203830e-05 1.641359e-05 -1.951938 0.0510386498- poly함수를 통해 각 열이 변수 age, age^2, age^3, age^4의 선형결합을 구할 수 있다.
- raw=TRUE 인자를 사용하면, age, age^2, age^3, age^4의 값을 직접 얻을 수 있다.
agelims=range(age)
age.grid=seq(from=agelims[1], to=agelims[2])
preds=predict(fit, newdata=list(age=age.grid), se=TRUE)
se.bands=cbind(preds$fit+2*preds$se.fit, preds$fit-2*preds$se.fit)
plot(age, wage, xlim=agelims, cex=.5, col='darkgrey')
title('Degree-4 Polynomial', outer=T)
lines(age.grid, preds$fit, lwd=2, col='blue')
matlines(age.grid, se.bands, lwd=1, col='blue', lty=3)
- 예측값을 원하는 age의 각 값을 생성하고, 그 다음에 표준오차도 제공하도록 명시하여 predict 함수를 호출한다.
fit.1=lm(wage~age, data=Wage)
fit.2=lm(wage~poly(age, 2), data=Wage)
fit.3=lm(wage~poly(age, 3), data=Wage)
fit.4=lm(wage~poly(age, 4), data=Wage)
fit.5=lm(wage~poly(age, 5), data=Wage)
anova(fit.1, fit.2, fit.3, fit.4, fit.5)
##Analysis of Variance Table
##
##Model 1: wage ~ age
##Model 2: wage ~ poly(age, 2)
##Model 3: wage ~ poly(age, 3)
##Model 4: wage ~ poly(age, 4)
##Model 5: wage ~ poly(age, 5)
## Res.Df RSS Df Sum of Sq F Pr(>F)
##1 2998 5022216
##2 2997 4793430 1 228786 143.5931 < 2.2e-16 ***
##3 2996 4777674 1 15756 9.8888 0.001679 **
##4 2995 4771604 1 6070 3.8098 0.051046 .
##5 2994 4770322 1 1283 0.8050 0.369682
##---
##Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1- 다항식의 차수를 결정하기 위해, 가설검정을 사용한다.
- anova함수를 사용하기 위해서는 model1과 model2가 내포 모델이어야 한다. 즉, model1의 설명변수들은 model2의 설명변수들의 서브셋이어야 한다.
fit=glm(I(wage>250)~poly(age, 4), data=Wage, family=binomial)
preds=predict(fit, newdata=list(age=age.grid), se=T)- 개인의 연간 소득이 25만 달러보다 더 높은지 예측한다고 가정해보면 다음과 같은 반응변수를 생성한 다음, family='binomial'옵션으로 다항식 로지스틱 회귀모델을 적합할 수 있다.
table(cut(age, 4))
##(17.9,33.5] (33.5,49] (49,64.5] (64.5,80.1]
## 750 1399 779 72
fit=lm(wage~cut(age, 4), data=Wage)
coef(summary(fit))
## Estimate Std. Error t value Pr(>|t|)
##(Intercept) 94.158392 1.476069 63.789970 0.000000e+00
##cut(age, 4)(33.5,49] 24.053491 1.829431 13.148074 1.982315e-38
##cut(age, 4)(49,64.5] 23.664559 2.067958 11.443444 1.040750e-29
##cut(age, 4)(64.5,80.1] 7.640592 4.987424 1.531972 1.256350e-01- cut함수는 다음과 같이 자동으로 절단점을 선택한다.
- break옵션을 사용하면 절단점을 직접 명시할 수 있다.
스플라인(Splines)
library(splines)
fit=lm(wage~bs(age, knots=c(25, 40, 60)), data=Wage)
pred=predict(fit, newdata=list(age=age.grid), se=T)
plot(age, wage, col='grey')
lines(age.grid, pred$fit, lwd=2)
lines(age.grid, pred$fit+2*pred$se, lty='dashed')
lines(age.grid, pred$fit-2*pred$se, lty='dashed')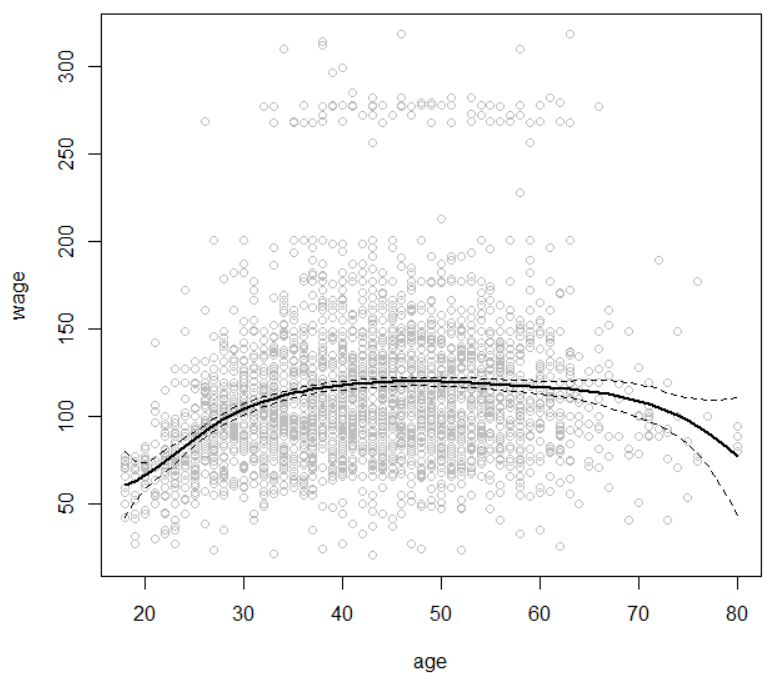
- 회귀 스플라인을 적합하기 위해 splines라이브러리의 bs함수를 이용한다. bs함수는 지정된 매듭(knots) 셋을 가진 스플라인들에 대한 기저함수들의 전체 행렬을 생성한다.
- 여기서 지정된 매듭은 25, 40, 60세이다. 이것은 6개의 기저함수를 가진 스플라인을 제공한다. (3개의 매듭을 가진 삼차 스플라인은 자유도가 7이며, 자유도 7은 절편과 6개의 기저함수에 의한 것이다.)
dim(bs(age, knots=c(25, 40, 60)))
##[1] 3000 6
dim(bs(age, df=6))
##[1] 3000 6
attr(bs(age, df=6), 'knots')
## 25% 50% 75%
##33.75 42.00 51.00 - df옵션을 사용하여 데이터의 균등 분위수에 매듭을 가지는 스플라인을 생성할 수 있다.
fit2=lm(wage~ns(age, df=4), data=Wage)
pred2=predict(fit2, newdata=list(age=age.grid), se=T)
lines(age.grid, pred2$fit, col='red', lwd=2)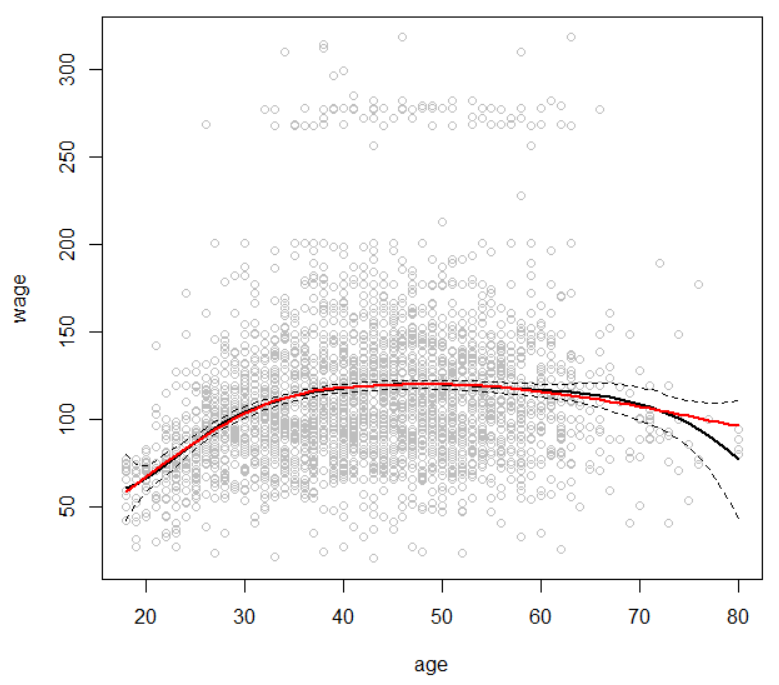
- 자연 스플라인(natural spline)을 적합하기 위해서는 ns함수를 사용한다. 다음은 자유도가 4인 자연 스플라인을 적합한다.
GAMs
gam1=lm(wage~ns(year, 4)+ns(age, 5)+education, data=Wage)
library(gam)
gam.m3=gam(wage~s(year, 4)+s(age, 5)+education, data=Wage)
par(mfrow=c(1, 3))
plot(gam.m3, se=TRUE, col='blue')- gam1은 year과 age의 자연 스플라인 함수를 사용하여 wage를 예측하도록 GAM을 적합한다. GAM은 적절히 선택된 기저함수를 사용하는 큰 선형회귀모델이므로 모델적합에 lm함수를 사용할 수 있다.
- gam라이브러리의 s함수는 평활 스플라인 사용을 나타내는 데 사용된다. year의 함수는 자유도가 4, age의 함수는 자유도가 5라고 지정한다.
- 이 그래프는 단순히 plot함수를 호출하면 만들 수 있다.

plot.Gam(gam1, se=TRUE, col='red')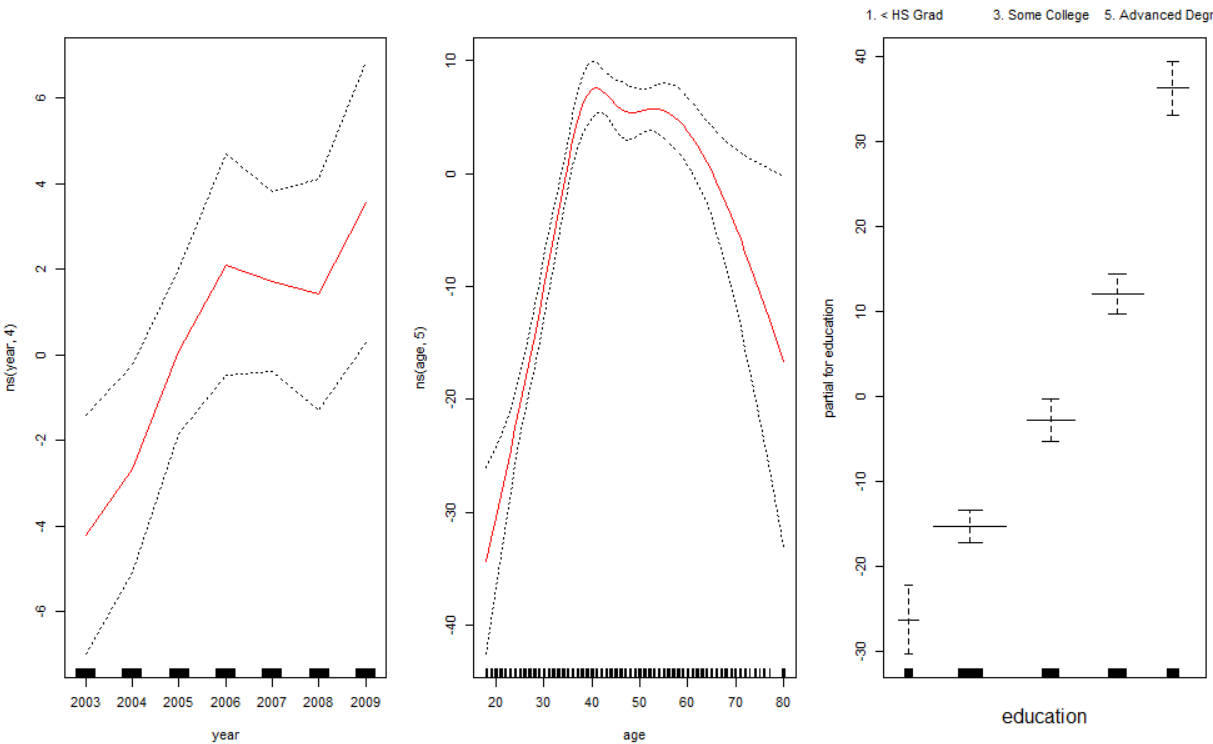
- lm클래스의 객체를 활용하기 위해서는 plot.Gam함수를 사용한다.
gam.m1=gam(wage~s(age, 5)+education, data=Wage)
gam.m2=gam(wage~year+s(age, 5)+education, data=Wage)
anova(gam.m1, gam.m2, gam.m3, test='F')
##Analysis of Deviance Table
##
##Model 1: wage ~ s(age, 5) + education
##Model 2: wage ~ year + s(age, 5) + education
##Model 3: wage ~ s(year, 4) + s(age, 5) + education
## Resid. Df Resid. Dev Df Deviance F Pr(>F)
##1 2990 3711731
##2 2989 3693842 1 17889.2 14.4771 0.0001447 ***
##3 2986 3689770 3 4071.1 1.0982 0.3485661
##---
##Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ - anova결과에 따르면 model2가 선호하는 모델이다.
스플라인, GAMs..... 학교다닐 때 안들었던 다변량.... 공부하기....
'머신러닝, 딥러닝' 카테고리의 다른 글
| [머신러닝] 7. 트리 기반의 방법- 배깅, 랜덤포레스트, 부스팅 (0) | 2021.09.11 |
|---|---|
| [R] 사용되지 않는 level 제거하기 (feat. drop.levels함수) (0) | 2021.05.10 |
| [머신러닝] 5. 선형모델 선택 및 Regularization- Ridge, Lasso regression, PCR, PLS (feat. R Code) (0) | 2021.04.25 |
| [머신러닝] 3. 분류- 로지스틱 회귀, LDA, QDA (feat. R Code) (0) | 2021.04.12 |
| [머신러닝] 2. 선형회귀분석- 고려해야 할 요소, 잠재적 문제(feat. R Code) (0) | 2021.04.04 |


